Wie Sie mit grosser Neugier feststellen konnten, haben wir ein neues statistisches Diagramm auf unserer Homepage etabliert. Es sind dies die sogenannten Box plots oder zu Deutsch Kastengrafiken. Wir wollen Ihnen diese Art von Diagramm im Folgenden anhand der Altersgruppe 30 bis 49 aus Deutschland vereinfacht erklären. (Falls Sie es schrittweise an einem Beispiel erklärt haben möchten folgen Sie diesem Link.)
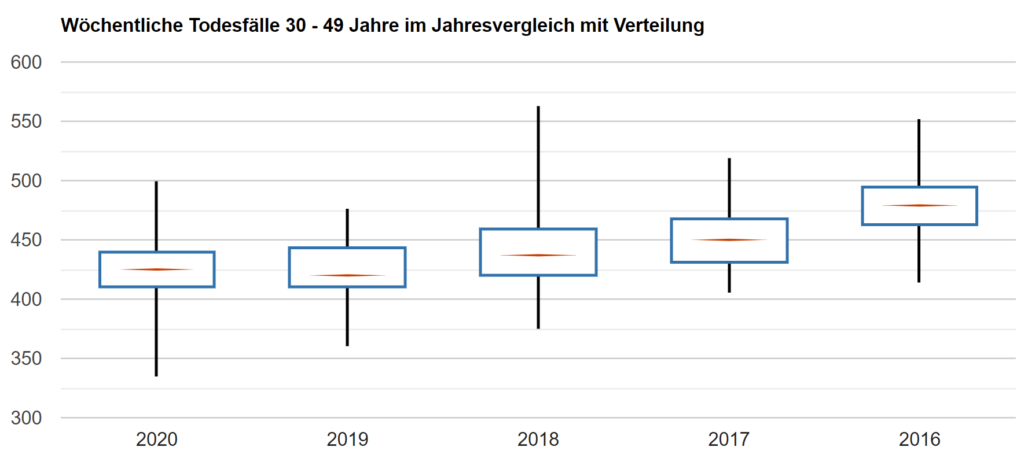
Die Kastengrafik basiert auf den wöchentlichen Todesfällen einer Altersgruppe. Diese wöchentlichen Todesfälle werden vom tiefsten bis zum höchsten Wert sortiert und auf der vertikalen Achse aufgetragen. Die Verteilung vom tiefsten bis zum höchsten Wert wird mit den schwarzen Linien dargestellt (Antenne). Somit erkennen Sie die tiefste und höchste Todesrate während eines Jahres. Für das Jahr 2020 und der Altersgruppe von 30 bis 49 in Deutschland wären dies ca. 330 für den Minimalwert und ca. 500 Fälle für den Maximalwert. Sie erkennen sofort, dass der Minimalwert tiefer ist als in den vier Jahren davor, wenn Sie die schwarzen Linien der einzelnen Jahre vergleichen.
Die rote horizontale Linie beschreibt den Median der wöchentlichen Todesfälle. Der Median für das Jahr 2020 beträgt 425. Der Median liegt in der Mitte der Zahlenwerte, wenn man die wöchentlichen Todesfälle der Grösse nach sortiert. (z.B. 4, 1, 37, 2, 1; der Median beträgt 2, da nach Grösse sortiert gilt: 1, 1, 2, 4, 37). Somit erkennen Sie sofort, dass der Median die wöchentlichen Todesfälle in zwei gleich grosse Gruppen einteilt. 50% der wöchentlichen Todesfälle sind kleiner als der Median und die restlichen 50% grösser als der Median.
Und nun zum namensgebenden Teil der Grafik, die Box. In dieser Box befinden sich genau die Hälfte aller Werte, welche den Median umgeben. Dh. 25% (oder ein Viertel) der Zahlenwerte befinden sich unterhalb des Medians (unteres Quartil oder 1st Quartile) und 25% der Zahlenwerte oberhalb des Medians (oberes Quartil oder 3rd Quartile). Unterhalb der unteren Linie der Box befinden sich die 25% tiefsten Zahlenwerte (unteres Quartil) und oberhalb der oberen Linie der Box befinden sich die 25% höchsten Zahlenwerte (oberes Quartil).
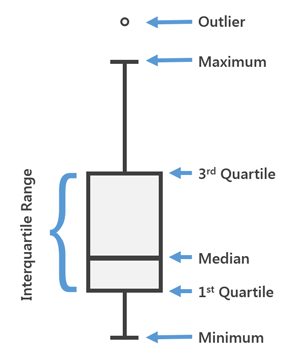
Was zeigt uns diese Darstellungsweise?
1) Die Verteilung vom kleinsten bis zum grössten Wert. Je länger die Antenne, desto grösser ist die Verteilung. Bei einer langen Antenne sind die Werte weiter gestreut und somit unterschiedlicher.
2) Der Median zeigt uns die Mitte der Werteverteilung an.
3) Die Box zeigt uns an, wie sich die Hälfte aller Werte um den Median verteilen. Je grösser die Box, desto grösser die Streuung und je kleiner die Box, desto kleiner die Streuung und ähnlicher die Werte.
Die Position des Medians und der Box gibt uns einen Hinweis, wie die Werte verteilt sind. Wenn der Median genau in der Mitte der Box und der Antenne liegt, sind die Werte gleichmässig verteilt (s. Beispiel Deutschland im Jahr 2020).
Falls der Median im unteren Bereich der Box liegt (s. Grafik oben oder Deutschland 2019), dann bedeutet dies, dass das obere Quartil eine grössere Streuung aufweist. Somit sind 25% der höheren Werte weiter gestreut und weisen hiermit einen grösseren Unterschied zueinander auf als die Werte unterhalb des Medians. Oder anders ausgedrückt, die Werte unterhalb des Medians (unteres Quartil) sind sich ähnlicher als die Werte des oberen Quartils.
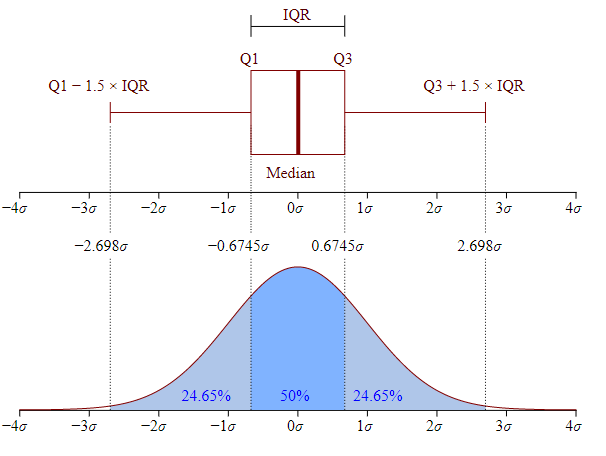
Die Darstellung oben beschreibt die Verteilung oder Streuung der Werte in einem symmetrischen Box plot Diagramm. Dabei erkennen Sie, dass die Hälfte aller Werte innerhalb der Box sind und die andere Hälfte ausserhalb der Box. Dabei gehören die Werte ausserhalb der Box entweder zu den tiefsten 25% (erstes Quartile, ganz links) oder zu den 25% höchsten Werten (drittes Quartile, ganz rechts).
Wenn nun eine Box nicht symmetrisch ist, dann ist die Verteilung verschoben. Dh. der Median befindet sich nicht in der Mitte der Box, somit ist die Verteilung und damit der Unterschied der unteren oder oberen Werte grösser als der oberen, respektive unteren Werte. Damit würde die Kurve in der oberen Grafik eine Schulter entsprechend nach links oder rechts aufweisen.
Wenn Sie die Grafiken der unterschiedlichen Altersgruppen betrachten, können Sie Vermutungen anstellen, ob die Pandemiemassnahmen in einer Altersgruppe einen Effekt haben (Median ist nach oben verschoben und Antenne ist nach unten verlängert) oder ob allenfalls eine Übersterblichkeit durch die Infektion überwiegt (Median ist nach unten verschoben und Antenne ist nach oben verlängert). Natürlich müssen Sie die Mediane vorhergehender Jahre vergleichen und gegebenenfalls das Bevölkerungswachstum miteinbeziehen, um einen akkuraten und zulässigen Schluss zu ziehen.