Mit grossem Wissensdurst lernten wir letztes Jahr das exponentielle Wachstum kennen. Ein Jahr später, der Wissensdurst ist noch immer gross und möchte erneut gestillt werden, trotz oder wegen DryJanuary.
Betrachten wir hierfür den asymptotischen Verlauf. Wie es die Definition bereits erklärt, nähern sich bei einem asymptotischen Verlauf die Werte immer näher einer Linie an, kreuzen diese jedoch niemals. Was das nun genau bedeutet und wie dies aussieht, zeigen wir anhand der Fallzahlen von Belgien. Belgien, erhielt die Silbermedaille in unserem Ländervergleich im Jahr 2020. Wir gehen davon aus, dass Belgien die Position aufgrund der hohen Bevölkerungsdichte inne hat.
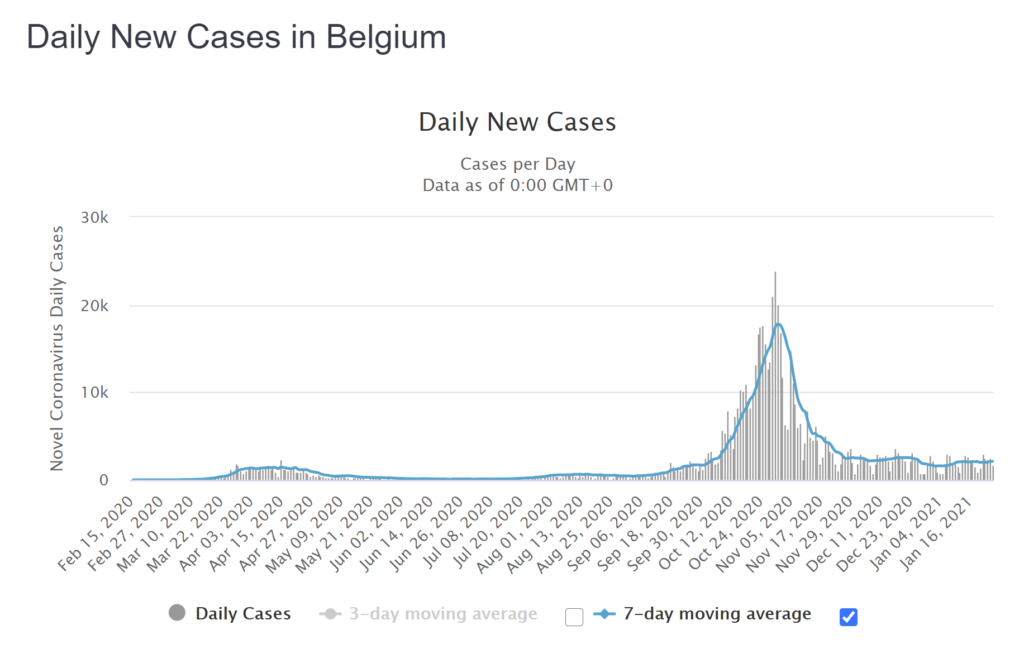
Was Sie nun mit grossem Schrecken feststellen dürfen, ist ein asymptotischer Verlauf der Coronafälle nach dem markanten Peak der zweiten Welle. Ein ähnlich asymptotischer Verlauf erkennen Sie auch zwischen den zwei Wellen, nur ist dieser weit geringer.
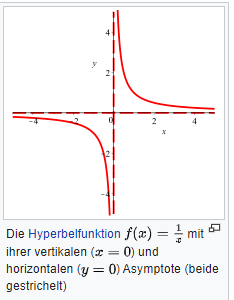
Ob es nun möglich ist, diese Fallzahlen in naher Zukunft weiter zu verringern, oder mit welchem Aufwand dieser asymptotische Verlauf reduziert werden kann, ist unklar. Daher haben wir mit den Fallzahlen aus Belgien ein Anschauungsbeispiel für den asymptotischen Verlauf einer Funktion, die sich immer mehr dem Nullwert annähert, diesen jedoch nicht unterschreitet. Es lohnt sich also, über Aufwand und Ertrag der Massnahmen nachzudenken. Um das Ganze mit einem weiteren abgedroschenen Wortspiel abzuschliessen, es könnte sein, dass viele dieser asymptotischen positiven Fälle auch asymptomatisch sind.